Members of Sublinear-time Algorithms Group
| Name | Affiliation | Role |
|---|---|---|
| Naoki Katoh | Kwansei Gakuin University | Project Leader |
| Kazuhisa Makino | Kyoto University | Member |
| Hiro Ito | The University of Electro-Communications | Member |
| Yoshio Okamoto | The University of Electro-Communications | Member |
| Yuichi Yoshida | National Institute of Informatics | Member |
| Toshiki Saitoh | Kobe University | Member |
| Yushi Uno | Osaka Prefecture University | Member |
| Atsushi Takizawa | Osaka City University | Member |
| Yuya Higashikawa | Chuo University | Member |
| Jinhui Xu | New York State University at Buffalo | Member |
| Yuki Kobayashi | Kyoto University | Research Assistant |
| Yoshihiko Ito | Kyoto University | Research Assistant |
| Adnan Sljoka | Kwansei Gakuin University | Postdoctoral Researcher |
| Naoya Takagi | Osaka City University | Research Assistant |
| Takuro Hatta | The University of Electro-Communications | Research Assistant |
| Tomohiro Imada | Kobe University | Research Assistant |
| Mikiya Imura | Tokyo Institute of Technology | Research Assistant |
| Munehiko Sasajima | Kwansei Gakuin University | Researcher |
Research Theme: Construction of Sublinear-time Algorithms for Big Data
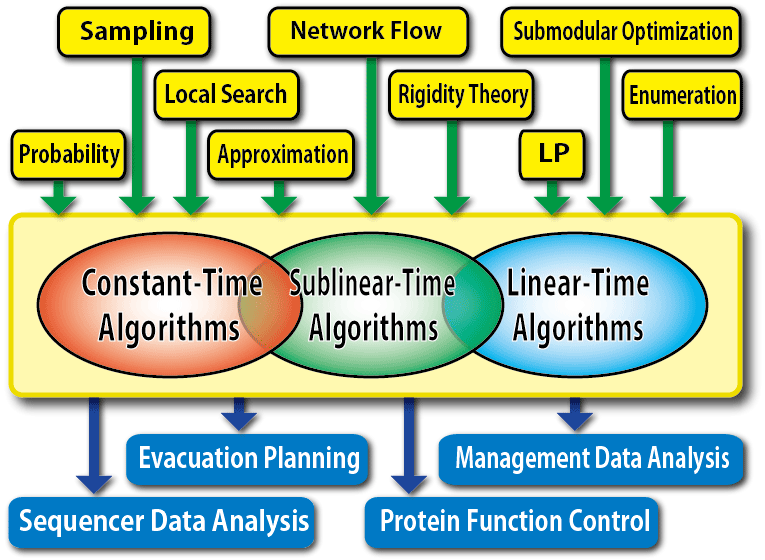 In this group, we propound a new computational paradigm, Sublinear-time Algorithm Paradigm, for big data.
We construct techniques for how to design algorithms and data structures,
and establish a foundation of innovative algorithms for big datum ages.
Especially, we develop linear or sub-linear time algorithms
for the fundamental problems which are often used as subroutines to solve actual problems,
for example searching, optimization, and enumeration problems,
by managing known techniques such as probabilistic, approximate and sampling methods.
Furthermore, we apply the algorithms to actual problems including
evacuation plan problems, for example the quick evacuation plan and assignment evacuation problems,
or protein function predictions by combinatorial rigidity.
In this group, we propound a new computational paradigm, Sublinear-time Algorithm Paradigm, for big data.
We construct techniques for how to design algorithms and data structures,
and establish a foundation of innovative algorithms for big datum ages.
Especially, we develop linear or sub-linear time algorithms
for the fundamental problems which are often used as subroutines to solve actual problems,
for example searching, optimization, and enumeration problems,
by managing known techniques such as probabilistic, approximate and sampling methods.
Furthermore, we apply the algorithms to actual problems including
evacuation plan problems, for example the quick evacuation plan and assignment evacuation problems,
or protein function predictions by combinatorial rigidity.
- Linear Time Algorithms In this research, we develop linear time Õ(n) (=O(n polylog n)) algorithms by using probabilistic approaches or concepts of approximations for the elemental problems which can be solved in polynomial time. Among them, we try to create the algorithms by focusing on the network problems such as the maximum flow problem or the minimum cost flow problem, the discrete optimization problems including the minimization problem of a submodular function, and the recognition problem of (k,l)-sparse graphs which has application for rigidity theory. To enhance utility of the algorithms, we improve the algorithms by applying heuristics. For instance, the maximizing submodular function problem is NP-hard and it is known that there is a greedy (1-1/e) approximation algorithm for the problem. Since this algorithm runs fast, we can apply the algorithm for the big data. On the other hand, the submodular function minimization problem has a lot of applications and there is a polynomial time algorithm. However, this algorithm runs in O(n6) time and it is hard to implement the algorithm because of the complication. Thus, we cannot apply the algorithm for the big data. The quick evacuation problem which is one of the important actual problems in our research can be reduced to the problem. Therefore, the development of the linear time algorithm for the problem is significant not only theoretically but also actually.
- Sublinear or Constant Time Algorithms Sublinear or constant time algorithms are frameworks, such that we solve problems by looking at a sliver of the data, that is, by using the o(n) or constant size of the data. Specifically, the constant time algorithms are ideal for treating the big data, since the algorithms treat only the constant size of the data even if the data is drastically huge. However, because the research of the constant time algorithms in the past was predawn, almost all of the results were in theoretical interests. This means that there are many in-practical algorithms which run in exponential towers by constant parameters, even the computational time is constant. It is important how the complexity of the constant time algorithms can be represented by the function for the approximation parameters, for considering the practical realization of the algorithms. Nevertheless, there have been no systematic and exhaustive research in these concepts previously.
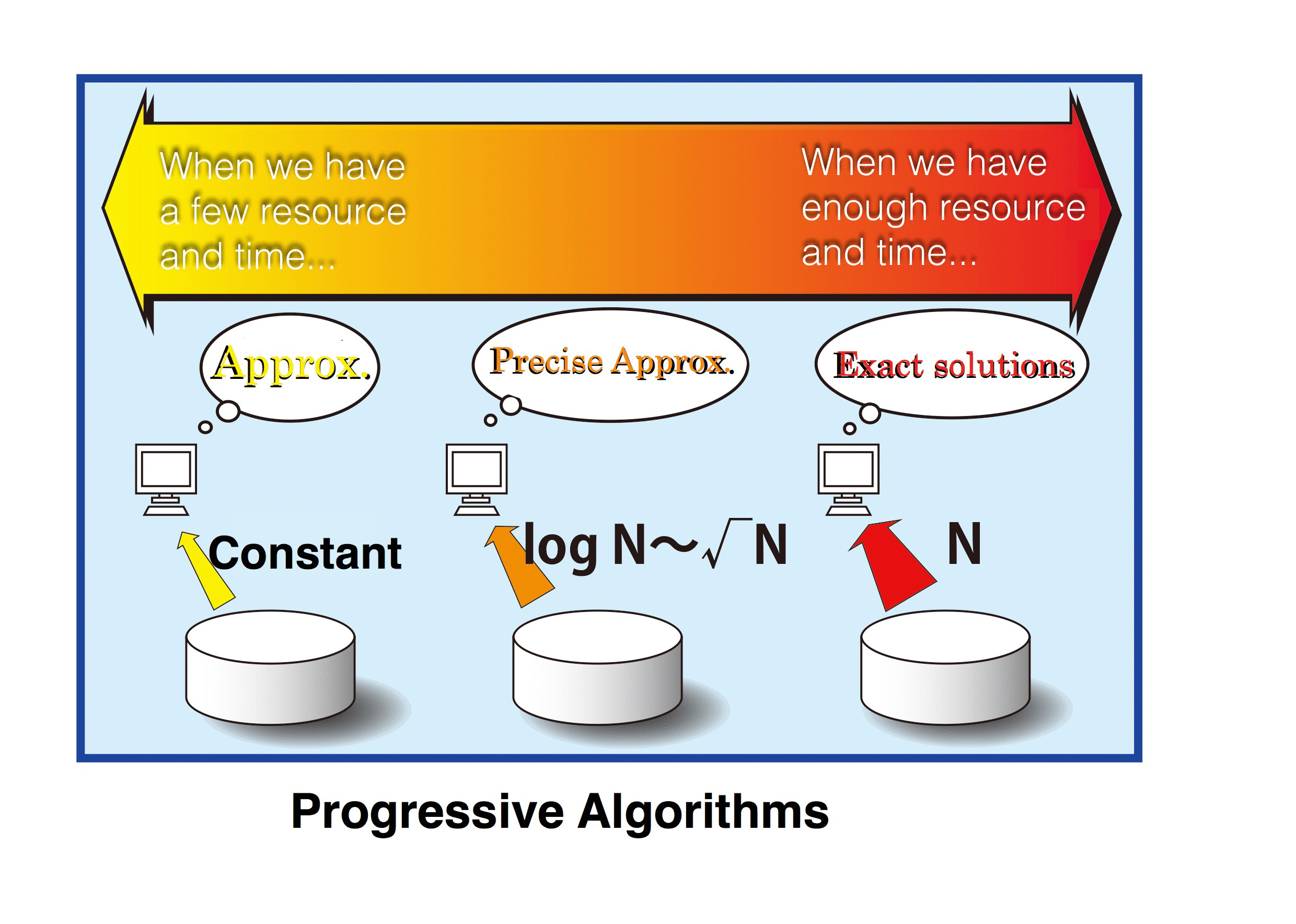
- Progressive Algorithms To deal with big data, we can consider this method: We first compute property of the data roughly from small size data, and then while increasing the data size, we make improvements to the precision of the results. Namely, we first compute property roughly by reading the data with constant size and then we obtain results depending on time and resources by increasing the data size to O(log n) and O(√n). We call the method progressive algorithms. In this research, we construct a theoretical basis of the progressive algorithms, verify the effect of the algorithms experimentally, and develop designing techniques of the algorithms.
- Evacuation Plan Problems In the evacuation plan problems, the goal is that we let as many people as possible go to secure places without congestion when disasters occur. These days it is common to use mobile devices such as smartphones or car navigation systems. There are some groped and implemented systems which are evacuation guidance using information and communication technologies. However, since the current systems are simple and guide us to the nearest evacuation from the position information of the mobile devices, the systems might not select suitable evacuation routes and locations for us. To achieve the effective evacuation, we have to collect and process information about where and how many evacuees are there or which routes are safe, globally and immediately.
- Protein Function Predictions by Combinatorial Rigidity It is significant to understand proteins deeply in biology, medical science, and pharmacy. To do this, we need to know the behaviors of proteins. It requires a high cost and a long time to experiment in order to know the behaviors, and computational methods based on the molecular dynamics method are not practical because the method takes too time consuming. On the other hand, by recent progress in rigidity theory, we could predict efficiently and accurately for the flexibility and the protein behaviors, and the results advanced in the area of the analysis of protein behaviors.
In this research, practical point of view for the big data, we develop algorithms such that the time complexity is represented by polynomial for the approximation parameters, and clarify practicality and its envelope of the algorithms. Concretely, we create fast constant time algorithms by using network properties, and verify practicality of the algorithms experimentally.
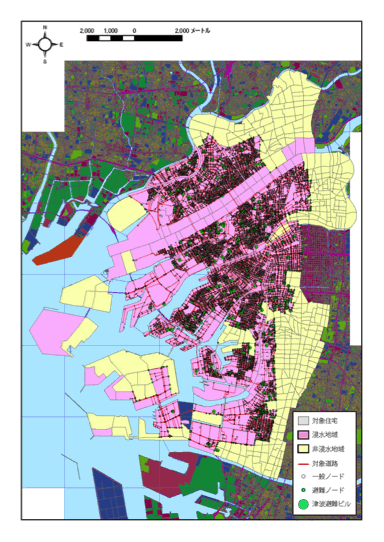
 In this research, for the evacuation plan,
we select Kansai region expected tsunami damage by Nankai Trough Earthquake
and we develop techniques to collect and process real-time data and develop theoretical evacuation plan models.
We implement the systems and verify practical effectiveness of them for the area.
Particularly, we deal with evacuation problems for underground malls,
assignments of evacuation centers, and wide-area evacuation from tsunamis.
In the evacuation problem for undergrad malls, we improve the research of time-expanded network,
and create and verify the large network models.
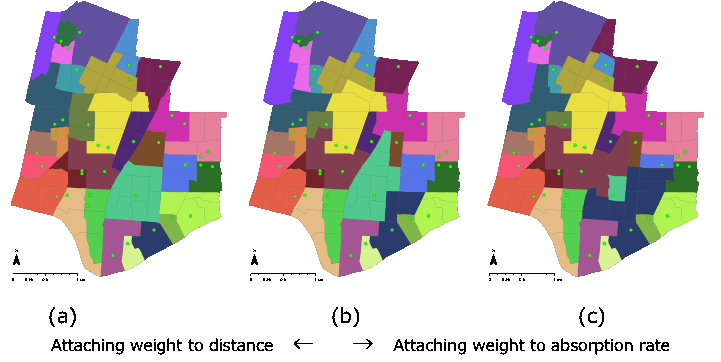
For the evacuation center assignment problem,
we develop approximation algorithms for extensive areas with the sublinear modeling group.
For the wide-area evacuation from tsunami, we simulate the tsunami flood by Nankai Trough Earthquake in high accuracy.
We construct time-expanded networks changing open areas with time from the data.
To solve the networks, we apply the improved algorithms being developed by this project for the maximum flow problem.
In this research, for the evacuation plan,
we select Kansai region expected tsunami damage by Nankai Trough Earthquake
and we develop techniques to collect and process real-time data and develop theoretical evacuation plan models.
We implement the systems and verify practical effectiveness of them for the area.
Particularly, we deal with evacuation problems for underground malls,
assignments of evacuation centers, and wide-area evacuation from tsunamis.
In the evacuation problem for undergrad malls, we improve the research of time-expanded network,
and create and verify the large network models.
For the evacuation center assignment problem,
we develop approximation algorithms for extensive areas with the sublinear modeling group.
For the wide-area evacuation from tsunami, we simulate the tsunami flood by Nankai Trough Earthquake in high accuracy.
We construct time-expanded networks changing open areas with time from the data.
To solve the networks, we apply the improved algorithms being developed by this project for the maximum flow problem.
In this research, we improve known algorithms by applying sublinear-time algorithms developed in this group. We develop methods to interpret the behaviors of huge scale proteins by collaborating with the sublinear data structure group. Especially, by using combinatorial rigidity theory, we focus on the understanding the behaviors of allosteric proteins and GPCR, and investigate the relationship of the behaviors and functions of the proteins.
