「平面上に赤点pn個、白点pm個が配置されている時(但し任意の3点は同一直線上に無いとする)、互いに重ならないp個の凸領域が存在し、各領域は丁度赤点n個、白点m個を含む様にできる」という金子、加納の予想を証明した。
本定理は、p=2とすると有名なハムサンドイッチ定理(但し2次元版)になり、それを一般化した重要な定理である。詳細は以下の文献で。
この結果の日本語による一般向けの解説文として
の4.10節 『2次元ハムサンドイッチ定理の一般化』
があります。
本結果は2007年発行の数学辞典第4版(岩波書店,日本数学会編)に掲載されました。
491 離散幾何学−B. 代表的なテーマと基本的な定理−2) 均等分割−8〜12行(P. 1610右側の段の中程)参照。
また、ハムサンドイッチ定理について詳しく知りたい方は、
等を御覧下さい。
将棋盤の大きさをn×nにし、王将を除く各駒の枚数をnの定数倍個用意した、一般化詰め将棋問題がNP困難であることを証明した。そしてさらに、還元玉と小駒図式と成駒無しの趣向を同時に満たすようにしてもなおNP困難であることを示した。この結果は、全ての詰め将棋を確実に解くアルゴリズムを作成することが非常に困難であることを示唆している。
参考文献
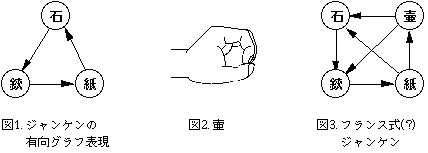
ジャンケンには石、紙、鋏の3つの手があり、石は鋏に勝ち、鋏は紙に勝ち、紙は石に勝つ。この関係は石、紙、鋏といった手を節点に対応させ、節点xに対応する手が節点yに対応する手に勝つときに有向枝(x,y)を持つような有向グラフによって一意に表わすことができる(図1参照)。噂ではフランスにはこの、石、紙、鋏に壷(図2参照)という手を加えた4手のジャンケンがあるらしい。これを有向グラフで表わせば図3になる。この様に、ジャンケンを拡張して考えると、様々な有向グラフに対して、対応するジャンケンが存在することになる。

有向グラフG=(V,E)が一般化されたジャンケンを表わすならば、任意の異なる2節点x,y \in Vに対して、(x,y)か(y,x)のどちらか一方がEに属している必要がある。この性質を満たす有向グラフを下記に定義する様にトーナメントと呼ぶ。
しかし任意のトーナメントがジャンケンとして使用可能かというとそうでは無い。
例えば図3のフランス式ジャンケンには重大な欠点がある。それは、石を出すくらいなら壷を出す方が絶対に有利、すなわち石も壷も共に鋏に勝ち紙に負けそして石は壷に負けてしまう、ということである。だから石は出す必要がなくなり、日本のジャンケンの石を壷と言い換えただけの同じジャンケンになってしまう。図3のジャンケンの石の様に、それを出すくらいなら他の手(この例では壷)を出した方が絶対に有利である様な手のことを無意味な手と呼ぶことにする。
我々は以下の定理を得た。
さらに我々は、面白いジャンケンとは、手の間に強弱のバラツキがあることであると考えた。例えば図4のT7とR7のジャンケンはともに手の数7で無意味な手は存在しない。しかしこの2つのジャンケンには大きな違いがある。それはR7は全ての節点が3つの節点に勝ち3つの節点に負ける(これを3勝3敗と表わす)のに対し、T7は0, 1, 2は3勝3敗だが、3は2勝4敗、4は4勝2敗、5は1勝5敗、6は5勝1敗と、ばらついていることである。
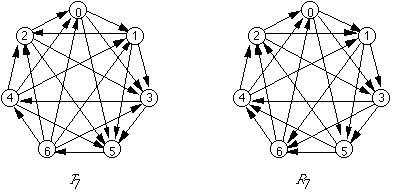
図4
この勝ち負けのばらつき方は、ジャンケンの面白さに大きく影響する。例えばR7のジャンケンを行なった場合、7つの節点はどれも本質的に同じなので、勝負をする人の心理としては、どれを出しても同じである。これは、節点数3つのジャンケンと(「あいこ」になる確率は減るものの)あまり変わらず、節点数を増やした意味が少ない。それに対してT7では、各節点の強さが異なるので、作戦の生じる余地がある。つまり、「6を出せば勝つ確率が高いので、出したいが、相手はそれを見越して、6に勝つ唯一の節点である(しかも6にしか勝たない)5を思い切って出すかもしれない。」等の駆け引きが生じるのである。トランプゲームでも、この様に節点間の強弱に変化をもたせて、面白さを出すのが、普通である(ナポレオン、戦争等)。節点の強さは、その節点が勝つ節点数と負ける節点数の差で表現できる。その強さのばらつき(分散)が、ジャンケンの面白さを決める1つの指針として、定義できる。
トーナメント(ジャンケン)G=(V,E)に対して、節点(手)x \in Vの強度s(x)をs(x)
= dout(x) - din(x) とする。ただし、dout(x)はxを始点とする枝数(=xが勝つ手の数)で、din(x)はxを終点とする枝数(=xが負ける手の数)。またGの面白さe(G)を、![]() で与える。
で与える。
これに対し、我々は、与えられた手の数nに対して、面白さe(G)が最大のジャンケンを構築する方法を示した、さらに我々が構築したジャンケン以外には(同型なものを除いて)面白さ最大のジャンケンは存在しないことも証明した。例えばT7は手の数7の面白さ最大の(しかも唯一の)ジャンケンであり、図5のジャンケンは手の数5の面白さ最大の(しかも唯一の)ジャンケンである。
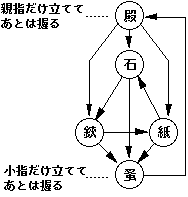
図5
本研究に関する文献としては下記のものがある。