本文中の基本的な用語については
滝根哲哉, 伊藤大雄, 西尾章治郎 著: 『ネットワーク設計理論』, 岩波講座『インターネット』第5巻, 岩波書店, 2001年6月7日刊行.
等の教科書を御参照下さい。
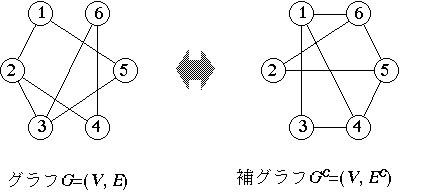
グラフG=(V,E) (但しVは節点集合でEは枝集合)を表現するのには通常\Theta(|V| + |E|)のデータ量が必要とされる。しかし(単純)グラフは補グラフ(complement graph)を用いても表現できる。すなわち図1のグラフGは、枝のある節点組と無い節点組を入れ替えてできた補グラフG^c=(V,E^c)を用いても表現できる。

グラフGの枝の数が多い場合には補グラフG^cを用いて表現した方がデータ量が少なくてすむ。すなわち従来\Theta(|V| + |E|)必要だったデータ量がO(|V| + min{|E|, |E^c|})ですむ。但し|E^c| =min{|E|, |V|(|V|-1)/2 -|E|})。この方法を利用すると、従来の高速アルゴリズムがさらに高速化される可能性が出てくる。例えば幅優先探索(breadth first search; BFS)と深さ優先探索(depth first search; DFS)は従来\Theta(|V| + |E|)時間必要とされていたが、グラフが本方法で格納されているとした場合、O(|V|+min{|E|, |E^c|})時間でできる。さらに
ということも示すことができる。
本研究について詳しくは文献
を参照されたい。
複数の倉庫に格納してある沢山の荷物を、倉庫からはみ出ないように(倉庫の隙間を利用して)入れ替える問題に対し、いくつか成果がある。下記文献参照のこと。
画像データは通常ピクセル毎に色(RGB)とその濃さのデータを持たせて表現する、これを色(RGB)毎に分けると後は濃淡を表現するだけなので、地形図を表現するように等高線で表現できる。この等高線表現を用いた場合において、画像に傷があった場合それをコンピュータでなるべく自然に見える様に修復するアルゴリズムを提案した。ここで、自然に、とは修復された等高線の長さの総和が最小になることとして定義した(実験の結果、この定義が妥当であることが確かめられた)。従来の画像表現法では自動化された自然な修復は困難であり、全て手仕事に頼っていた。等高線表現を用いたことによって、自然な自動化アルゴリズムが達成されている。詳細は下記文献参照。
なお、本研究において、画像を等高線表現して等高線の総和最小によって自然な修復アルゴリズムを達成するという基本的なアイデアは筆頭著者の浅野哲夫教授(北陸先端大)によるもので、伊藤は最適性を保証する高速アルゴリズムを提案することによって貢献している。
種々の設備管理システム等でコンピュータディスプレイ上に地図を表示する際に、大都市等の設備が集中している場所を拡大表示し、設備の少ない場所を縮小表示したいことがある。これを一つの地図を変形して自然に表示することは、駅すぱあとなどのコンピュータソフトでも自然に取り入れている。通常この変型は手仕事でなされているが、ある程度複雑な地図を変形するためには専門的な技術が要求されるため、素人では難しい。よってこれを自動化するアルゴリズムについて考察した。変形法が悪いと利用者にとってとても見辛いものとなるため、見易い変形を、設備間の東西南北関係が入れ代わらないこと、と定義し、この制約のもとで限られた画面内で各設備間の距離がなるべく大きくなる様に変形するアルゴリズムを提案した。本研究について詳しくは下記文献参照のこと。